Model Development and Evaluation
Model Development
Kita telah menentukan variabel mana yang bagus mana yang jelek. Kita juga sudah membersihkan data sehingga akhirnya siap untuk digunakan dalam pengembangan model. Sekarang saatnya kita memprediksi harga mobil berdasarkan data yang ada.
Buka hands-on di github atau langsung buka di colab
Simple dan Multiple Linear Regression
- (Simple) Linear regression mengacu pada satu variabel independen untuk membuat prediksi
- Multiple linear regression mengacu pada lebih dari satu variabel independen untuk membuat prediksi
Simple Linear Regression
Ini hanya untuk dua variabel saja, satu prediktor satu target.
\[Y=a+bX\]Dimana:
- \(a\): intersep (nilai ketika x=0)
- \(b\): slope (kemiringan garis/gradien)
Prediction
Anggaplah highway-mpg punya relasi linear dengan price.
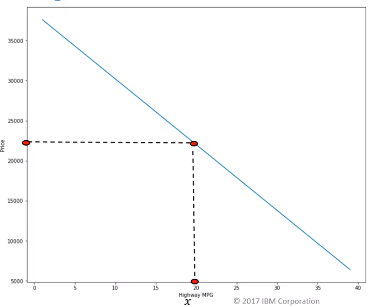
Jika highway-nya 20 maka pricenya sekian.
Fitting
Nah untuk membuat garisnya. Diambil titik data untuk di latih (fit).
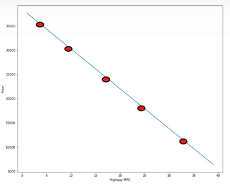
Hasil dari fitting adalah parameter \((a,b)\).
Titik data disimpan dalam numpy array. Array y untuk target, array x untuk predictor.
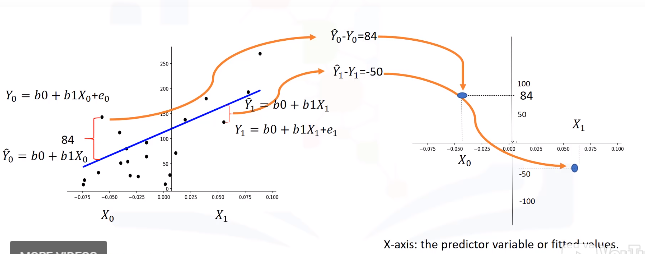
Banyak faktor yang dapat mempengaruhi prediksi. Ketidakpastian ini disertakan dengan mengasumsikan nilai acak kecil ditambahkan pada titik data di garis regresi. Inilah yang disebut noise.
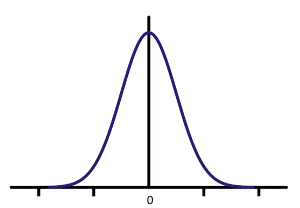
Gambar di atas adalah distribusi noisenya
- Sumbu vertikal menunjukkan value yang ditambahkan
- Sumbu horizontal mengilustrasikan kemungkinan value tersebut akan ditambahkan
Wrap Up
- Kita punya training point (titik data untuk dilatih)
- Kemudian di train
- Menghasilkan parameter \((a,b)\)
- Gunakan parameternya untuk model \(\hat{Y}=a+bX\)
Jika masih penasaran dengan cara kerja linear regression, video dibawah mungkin bisa membantu
Fitting a Simple Linear Model Estimator
from sklearn.linear_model import LinearRegression
Kemudian bikin objek
lm = LinearRegression
Tentukan variabel prediktor dan target nya
X = df[['highway-mpg']]
Y = df['price']
Kemudian fit the model
lm.fit(X,Y)
Sekarang kita bisa memperoleh prediksi
Yhat = lm.predict(new_predictor)
\(a\) dan \(b\) dapat diakses sebagai atribut.
Multiple Linear Regression
Z = df[['horsepower', 'curb-weight', 'engine-size', 'highway-mpg']]
lm.fit(Z, df['price'])
Yhat = lm.predict(new_predictor)
Model Evaluation dengan Visualisasi
Regression Plot
Kenapa pakai regression plot?. Karena bisa memberi estimasi yang bagus pada:
- Relasi antara dua variabel
- Tingkat korelasi
- Arah relasi (positif atau negatif)
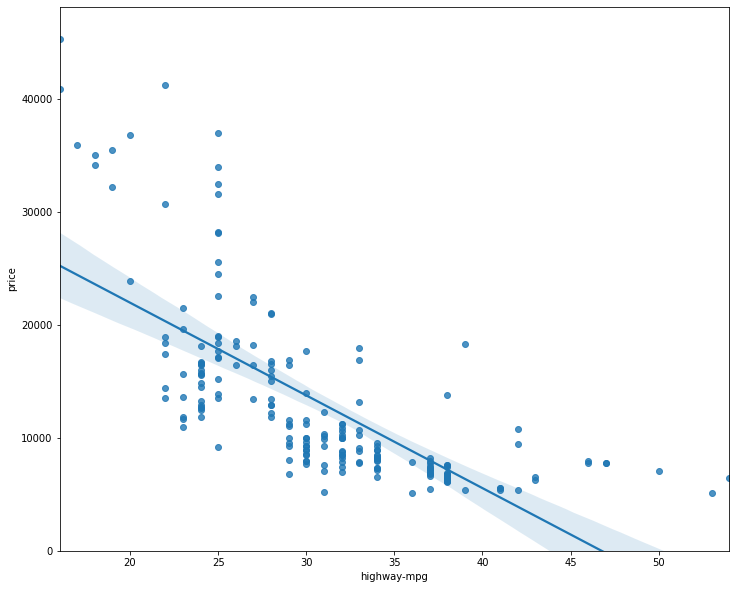
Regression plot dapat menampilkan kombinasi dari scatter plot dan garis regresi linear yang sudah dilatih. Garis regresi linear merepresentasikan nilai yang diprediksi.
Cara menggunakannya
import seaborn as sns
sns.regplot(x="highway-mpg", y="price", data=df)
Residual Plot
Residual plot merepresentasikan error antara nilai aktualnya.
Kurangkan nilai actualnya dengan nilai predicted-nya sehingga dapat nilai error. Kemudian plot kembali hasilnya.
Hasil yang diinginkan adalah plot nya (titik-titiknya) tersebar secara random disekitar sumbu x.
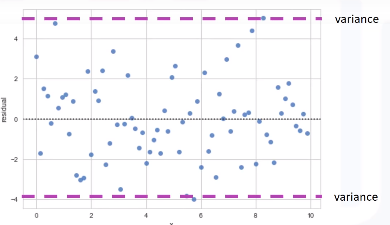
Ini berarti linear modelnya bagus.
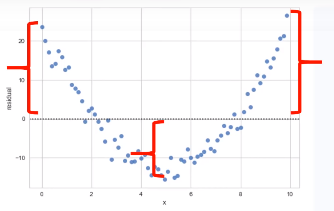
Disini plotnya membentuk kurva, tidak tersebar secara random. Mungkin lebih baik menggunakan nonlinear model.
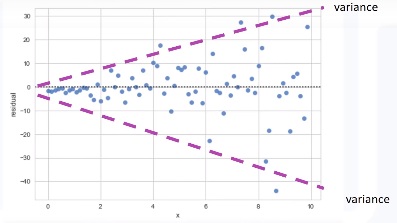
Disini variance dari residualnya meningkat dengan x. Maka model nya salah
import seaborn as sns
sns.residplot(df['highway-mpg'], df['price'])
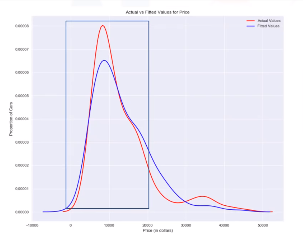
Distribution plot
Distribution plot menghitung nilai actual versus nilai predicted.
import seaborn as sns
ax1 = sns.distplot(df['price'], hist=False, color="r", label='Actual value')
sns.distplot(Yhat, hist=False, color='b', label='Fitted Values', ax=ax1)
Polynomial Regression dan Pipelines
Polynomial regression
Bagaimana jika linear regression bukan model yang tepat. Kita ubah data kita menjadi polinomial (suku banyak) kemudian gunakan linear regression untuk melatih parameter
Polynomial regression berguna untuk relasi yang berbentuk kurva (curvilinier relationship). Curvilinier relationship didapat dari mengkuadratkan atau menetapkan derajat suku tinggi ke variabel prediktor. Berarti harus transforming data.
Walaupun variabel prediktor dari Polynomial Regression tidak linear, hubungan antara parameter atau koefisien nya tetap linear.
Macam-macam polynomial regression
- Quadratic - derajat 2
- Cubic - derajat 3
- Derajat tinggi
Implementasi di Python
Menghitung polynomial derajat 3
f = np.polyfit(x,y,3)
p = np.polyfit(f)
Dimensi banyak
\[\hat{Y} = b_0 + b_1 X_1 + b_2 X_2 + b_3 X_1 X_2 + b_4 (X_1)^2 + b_5(X_2)^2 + \dots\]from sklearn.preprocessing import PolynomialFeatures
pr = PolynomialFeatures(degree=2, include_bias=False)
x_polly = pr.fit_transform(x[['horsepower', 'curb-weight']])
Pre-processing
Semakin besar dimensinya (variabel yang digunakan), kita mungkin mau menormalisasikan fitur-fitur (variabel) nya sekaligus.
from sklearn.preprocessing import StandardScaler
scale = StandardScaler()
scale.fit(x_data[['horsepower', 'highway-mpg']])
x_scale = scale.transform(x_data[['horsepower', 'highway-mpg']])
Pipeline
Pipeline digunakan untuk menyederhanakan proses
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
# buat list of tuple
# elemen pertama adalah namanya
# elemen kedua adalah constructornya
input = [('scale', StandardScaler()), ('polynomial', PolynomialFeatures(degree=2)), ..., ('model', LinearRegression())]
#pipline constructor
pipe = Pipeline(input)
# we can train the pipeline object
pipe.train(x[['horsepower', 'highway-mpg', 'curb-weight', 'engine-size']], y)
yhat = pipe.predict(X[['horsepower', 'highway-mpg', 'curb-weight', 'engine-size']])
Metode ini menormalisasi data, transformasi polinomial, dan menghasilkan prediksi.
R-Squared dan MSE untuk In-Sample Evaluation
Pengukuran ini adalah salah satu cara untuk mengukur secara numerik seberapa bagus modelnya untuk dataset. Ada dua metrik pengukur penting:
Mean Squared Error (MSE)
Langkahnya:
- Selisihkan nilai asli dan predicted nya
- Pangkatkan 2
- Tambahkan dengan nilai-nilai yang lain
- Bagi sejumlah banyak nilai-nilainya
from sklearn.metrics import mean_squared_error
mean_squared_error(df['price'], Y_predict_simple_fit)
R-Squared
Disebut juga Coefficient of Determination adalah pengukuran untuk menentukan seberapa dekat data dengan garis regresi.
\[R^2=1-\frac{MSE\ of\ regression\ line}{MSE\ of\ the\ average\ of\ the\ data}\]1 artinya bagus, 0 jelek
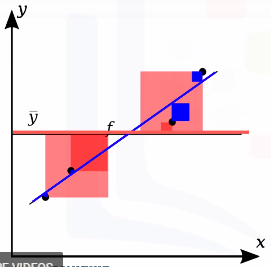
- Garis biru merepresentasikan garis regresi
- Kotak biru menunjukkan MSE dari garis regresi
- garis merah menunjukkan rata-rata nilai dari titik data
- Kotak merah menunjukkan MSE dari garis merah
- Bisa dilihat kotak biru lebih kecil daripada kotak merah
R-Squared di python dapat diakses dari atribut score model object setelah di fit
Prediction dan Decision Making
Prediction
Prediksi bisa dilakukan dengan memasukkan nilai X yang mau diprediksi ke dalam method predict
yhat=lm.predict(new_input)
Menentukan Model yang Bagus
Supaya tau model ini adalah best fit, lihat:
- Nilai yang diprediksi makes sense, misalnya nilai nya tidak negatif
- Visualisasinya
- Pengukuran numerik untuk evaluasi
- Membandingkan antara model yang berbeda
- Apakah MSE yang lebih rendah selalu mengindikasikan model lebih baik? Belum tentu
- MSE untuk model Multiple Linear Regression akan selalu lebih kecil daripada MSE untuk Simple Linear Regression. Karena error pada data akan berkurang ketika lebih banyak variabel yang dimasukkan ke dalam model
- Polynomial Regression juga akan punya MSE yang rendah daripada linear regression biasa
- Hubungan kebalikannya yang serupa juga berlaku untuk R-Squared
Model Evaluation and Refinement
Evaluasi model dibutuhkan untuk mengukur akurasi. Akurasi model dapat ditingkatkan dengan banyak metode.
Buka hands-on model evaluation di github atau langsung buka di colab